Part 11. Revisit of the HPLinpack benchmark

content by Xing Chen

The HPLinpack benchmark for Top500 list, introduced by Jack Dongarra, generates a random n by n dense linear system of equations Ax = b, then measures how fast a computer can solve it. The main steps of the benchmark are:

1. Generates a random n by n dense linear system Ax = b;

2. Compute the LU factorization with row partial pivoting of the n-by-n+1 coefficient matrix [A b] = [[L,U] y]. Since the lower triangular factor L is applied to b as the factorization progresses, the solution x is obtained by solving the upper triangular system U x = y, by using the Backward Substitution.

3. Verify the result: a solution is considered as “numerically correct” when the backward error is less than a threshold value of the order of 1.0. In the formula below, ε is the relative machine precision (according to IEEE754, ε is ½53 for FP64) and n is the size of the problem. This implies the computation must be done in 64bit floating point arithmetic, the FP64.

Backward-error=||Ax-b||∞ / (||A||∞ ||x||∞ + ||b||∞) / (n * ε)

More details can be found here:

https://www.netlib.org/benchmark/hpl/algorithm.html

https://www.netlib.org/utk/people/JackDongarra/PAPERS/hpl.pdf

I spent three parts (7, 8, & 9) discuss the SIMD, here the D stands for Data, and it means IEEE754 FP64 for modern CPUs. Because HPLinpack has to run with FP64, so, at the end, what the Linpack benchmark really measures is the CPU SIMD extension’s performance (and the GPU’s FP64 performances, should the to be benchmarked system is equipped with GPUs, either the NVIDIA or the AMD one, as long as they support FP64 arithmetic).

It is also shown that the precision of the final solution is related with the used data type, as shown by the formula to calculate the backward error, which contains ε, the used data type precision. In theory, use high bit count data type normally always give high precision; in other words, higher precision is achievable with FP64 than with FP32, than with FP16 (if the application can work with them), thus, there are always the interest to use high bit count data types, such as FP64, or even FP128, for scientific computing.

Since years, there is a new market trend: with the proliferation of AI, there are more and more hardware which are with low bit count data types, mainly used to deal with AI computing needs, as shown by the following table.

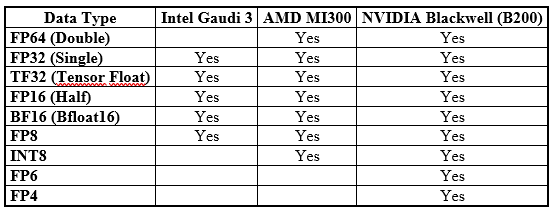
The operations involving these low bit count data types can be executed very fast, more importantly, with high energy efficiency, because usually they are executed as matrix operations by using matrix arithmetic units, such as the Intel MMX (Matrix Multiplication Engine), AMD Matric Core, and Nvidia Tensor core.

The question is: Can these low bit count operations and the corresponding matrix arithmetic units be used for scientific computing, which were always in favor of high bit counts?